The new Vulkan Coordinate System

Matthew Wellings 20-Mar-2016

Vulkan introduces a number of interesting changes over OpenGL with some of the key performance and flexibility changes being mentioned often on the internet. A more subtle yet equally important change to be understood is the that of the coordinate system.

The first change of note is that the y axis now points down the screen. The x and z axes point in the same direction as before. This means that if you do not correct for this two notable things happen. Firstly your image will be flipped. Secondly your face culling order will be backwards. There are multiple ways of resolving this. The method used in the samples is to simply add the following line to all vertex shaders:

gl_Position.y = -gl_Position.y;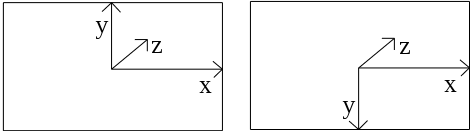

In OpenGL we had a left-hand NDC space, in Vulkan we have a right hand NDC space (assuming depth clear value is 1 and depth function is GL_LEQUAL / VK_COMPARE_OP_LESS_OR_EQUAL).

The other change to the coordinate system is to the z axis i.e. the depth range. After the programmable vertex stage a set of fixed function vertex operations are run. During this process your homogeneous coordinates in clip space are divided by w_c (to give NDC space) and then transformed into window space (now called framebuffer space).

The divide by w_c is the first of these two steps and has not changed but the transformation into window space has.

OpenGL expected a final depth range for z_w of [0-1]. The standard perspective projection matrix transforms points on the near plane to have a z_d value of -1 and points on the far plane to have a z_d of 1.
These were placed into the range [0-1] by the transform into window space. In OpenGL this transform was defined as:

$\left(\begin{array}{c}{x}_w\\ y_w\\ z_w\end{array}\right)=\left(\begin{array}{c}\frac{p_x}{2}{x}_d+o_x\\ \frac{p_y}{2}{y}_d+o_y\\ \frac{f-n}{2}{z}_d+\frac{n+f}{2}\end{array}\right)$

Where z_d is z_clip/w_clip and f and n were set using glDepthRange(double n, double f). The default values of n and f were 0 and 1 respectively. Substituting in these defaults the z component of this transform simplifies to ½z_d + ½.

In Vulkan the transform is now defined as:

$\left(\begin{array}{c}{x}_f\\ y_f\\ z_f\end{array}\right)=\left(\begin{array}{c}\frac{p_x}{2}{x}_d+o_x\\ \frac{p_y}{2}{y}_d+o_y\\ p_z\times z_d+o_z\end{array}\right)$

Where z_d is still z_clip/w_clip, p_z = maxDepth-minDepth and o_z = minDepth. The maxDepth and minDepth values are as set in your VkViewport.

If you have your minDepth and maxDepth to 0 and 1 respectively, your near plane will be at -2fn/(f+n) where f and n are the near and far parameters used to create your perspective matrix (probably not what you want).

Many Vulkan demos do set the minDepth and maxDepth to 0 and 1 respectively and use another line of code at the end of the vertex shader:

gl_Position.z = (gl_Position.z + gl_Position.w) / 2.0;

This code works because once you divide (z_c+w_c)/2 by w_c and rearrange you get z_d = ½(z_c/w_c) + ½.
Applying the Vulkan transform of p_z * z_d + o_z with p_z=1, and o_z=0 you still get z_f = ½(z_c/w_c) + ½. This is the same transform as OpenGL with default depth range.

It is also worth mentioning that so-far we have only discussed the final window/framebuffer coordinates & depth range. These are used for bounding, storage and testing. There is also the clipping stage which happens in homogeneous clip space (immediately after the vertex shader, before the divide by w_c). OpenGL defined its clip volume's z bounds as -w_c ≤ z_c ≤ w_c but they are now defined in Vulkan as 0 ≤ z_c ≤ w_c. Using this line in your shader will also give the correct values in clip space as it shifts points on the near plane to z_c=0.

There are some alternatives to adding these lines to the end of your vertex shaders. One of these is to pre-multiply your projection matrix by the following correction matrix:

$\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& -1& 0& 0\\ 0& 0& 1/2& 1/2\\ 0& 0& 0& 1\end{array}\right]$

The resulting corrected projection matrix is mathematically equivalent to using these two shader lines but does not require the additional GPU overhead.

LunarG have an example of the use of this matrix in their Hologram demo.

If you are using Glm you may be interested in the new define GLM_FORECE_DEPTH_ZERO_TO_ONE. This define will give you the correct depth range but still leave the y direction reversed.

Further Reading

Vulkan Spec sections 23.2, 23.3 and 23.5 Khronos
OpenGL Spec sections 13.5 and 13.6 (PDF) Khronos

Comments

Show Comments (Disqus).

Stats

Loading stats...

Matthew Wellings - Blog

Follow @WellingsMatt

Depth Peeling Pseudo-Volumetric Rendering 25-Sept-2016
Depth Peeling Order Independent Transparency in Vulkan 27-Jul-2016
The new Vulkan Coordinate System 20-Mar-2016
Improving VR Video Quality with Alternative Projections 10-Feb-2016
Playing VR Videos in Cardboard Apps 6-Feb-2016
Creating VR Video Trailers for Cardboard games 2-Feb-2016
Playing Stereo 3D Video in Cardboard Apps 19-Jan-2015
Adding Ray Traced Explosions to the Bullet Physics Engine 8-Oct-2015